Rounding functions in Excel

Rounding numbers involves replacing a number with one of approximately the same value but with fewer digits. Rounded numbers do therefore inherently introduce a certain level of inaccuracy into calculations which can become an issue, for example when completing a business model spreadsheet, so at the end of the blog some of the alternatives to using a rounding function will be discussed.

There are however several functions that can be used to round numbers in Excel and which one you pick depends on whether you want to round up, down or just to the nearest integer or chosen multiple. This blog will look at the variety of rounding functions, how to use them and what results you can expect to get!

The Integer function

This isn't really a rounding function at all in that it simply removes any decimals from a number - i.e., both 17.34 and 17.98 would end up as 17 (this is also known as truncation). The syntax for the INT function is very straightforward and the only argument needed is the number or the cell reference to the number that needs to be converted to a whole number:

Certainly decimal places could be shown again by using a suitable number format (as below) but the output of the INT function can only ever be a whole number:

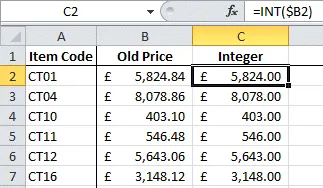
The INT function effectively rounds down to the nearest whole number.

The Round function

ROUND is a more sophisticated way of rounding numbers and works on the accepted principle that 0.5 and above rounds up while anything less than 0.5 rounds down (this is also known as the round half up rule). The ROUND function consists of two arguments, the number to be rounded and the decimal place to which rounding is required:

A value of 0 for Num_digits would return the nearest integer, a value of 1 returns to the nearest single decimal place, 2 to the second decimal place and so on:

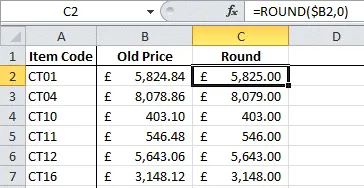
Num_digits has nothing to do with cold fingers.

If you needed to round to the nearest multiple of 10 or 100 you can use -1 or -2 in the Num_digits argument to achieve that result:

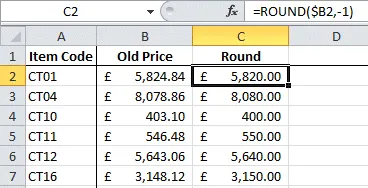
If you added -0.01 to the end of the formula, all your prices would be rounded to the nearest £XXX9.99!

Rounding up or rounding down?

If you need the ability to specify decimal accuracy but want to force the calculation to either always round up or round down then consider the ROUNDUP and ROUNDDOWN functions.

These two functions are pretty self-explanatory and use the same arguments as ROUND, i.e. the number to be rounded and the required decimal accuracy. In the example below both functions have a Num_digits value of 0 so that they return the appropriate integer:

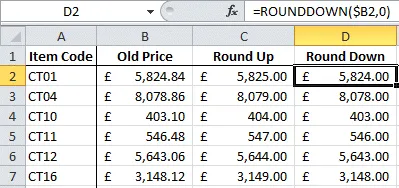
ROUNDUP and ROUNDDOWN override the round half up rule.

Rounding to a given multiple

Sometimes you might wish to round to a multiple of a specified amount that isn't 1, 10, 0.1 and so on (which can be achieved with the standard ROUND function shown above). If you wished to round to the nearest multiple of, say, 2 then the best function for this would be MROUND.

Like ROUND, MROUND also works on the round half up principle. This would mean that if you wanted to round to the nearest multiple of 15, then 7.5 would round up to 15 whereas 7.49 would round down to 0. Similarly 22.5 would round to 30 and 22.49 down to 15. The syntax for the MROUND function is as follows:

In the example below a rounding multiple of 2 has been used:

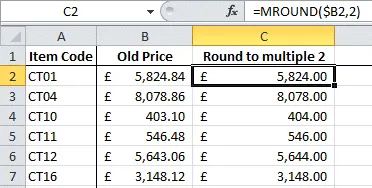
The effect of the formula in this example is to round to the nearest even integer.

Up to the ceiling or down to the floor

The last pair of rounding functions combine multiple rounding with the ability to decide whether all numbers should be rounded up or rounded down to the given multiple (known as the multiple of Significance in these functions).

The CEILING and FLOOR functions consist of the same two arguments as the MROUND function above but will round up or down respectively. The syntax for these functions is shown below:

In use, these functions would give the following series of results:

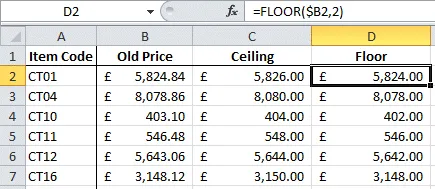
Both these functions round to a specified multiple.

Problems with rounded numbers

As mentioned at the beginning of the article, errors can quickly creep into calculations if several rounded numbers are used in sequence. The table below may be short but proves how inaccuracies could rapidly build up, making column totals or other calculations meaningless:

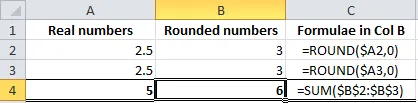
Note that the SUM calculation isn't itself rounded, but the numbers it is adding up are.

The effect of rounding in the above table is admittedly made worse by the choice of numbers. When a column consists of many numbers, some of which will be rounded up and some of which will be rounded down based on the round half up principle, the sum of those numbers may well be not too inaccurate. Of course, if a totally asymmetric rounding function is employed, such as ROUNDUP or ROUNDDOWN, then the errors are greatly increased. Summing is only part of the story though, and if multiplier values were rounded and then used several times within a calculation it is easy to see how considerable inaccuracies can occur.

Consequently, it could be regarded as best practice to avoid using rounding functions completely, or at least reserving them for the final figure, and instead utilising some number formatting tricks to show the style of number required without affecting the underlying value.

Using number formatting to round the visible number

The alternative to using a function to round a number would be to change its format. An obvious example of this would be when using the Currency or Accounting formats which, by default, round to two decimal places. While this can still lead to visual errors, the full number is held in the spreadsheet so that mathematical errors will not accumulate:

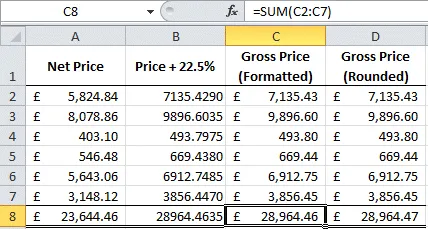
While the total for the formatted column doesn't look like it has added up correctly (1p short!), the answer is in fact more accurate that the total based on the rounded numbers in column D.

As well as using the preset number formats in Excel, a common use of custom number formatting would be to show large numbers in thousands (k) or millions (m). By using such formatting, the number £25,478,329.12 could be shown to be approximately £25.5m, though the original number would still be used in other calculations. If the number had been rounded to that figure with a function, or combination of functions, it is clear that the potential inaccuracies could be huge.

The example below shows the custom format discussed above:

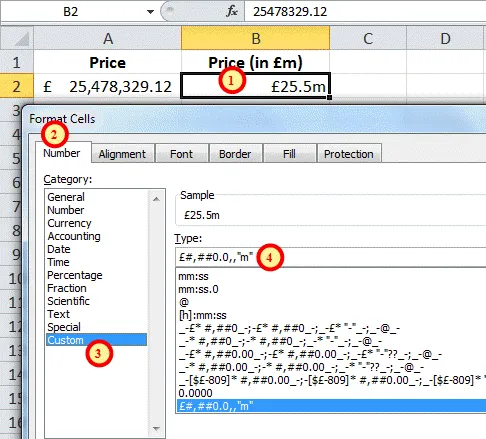
Follow the steps below to create this format.

1. Right click on the cell that needs to be formatted and open the Format Cells dialog box

2. Click on the Number tab.

3. Choose the Custom category.

4. Enter the format shown in the Type field. Each comma is a thousands separator, so the last two lots of thousands are not shown, and the text to be added must be bounded by speech marks.